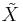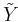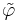W. Dembski introduces two programs in his post
The original weasels at his blog
Uncommon Descent. These programs were sent to him by someone called
Oxfordensis, and W. Dembski states
These are by far the best candidates [for being Dawkins's original program] we have received to date.
Let's have a short look:
Weasel 1
Here's how this program works for the target "METHINKS IT IS LIKE A WEASEL":
- Chose random string
- copy string 100 times, each time changing exactly one letter at random
- select string with most correct letters in place
- is the number of correct letters 28? Then STOP. Otherwise:
- goto 2
The mutation procedure is interesting: While most programs I've seen mutate the parent string by changing each letter with a certain probability, here, exactly one letter is changed - but I've seen implementations of this version, too. The letter-based mutation seems to be more natural, while the other one has mathematical advantages: the neighbourhood of a string
s, i.e., the strings
s can mutate into, becomes small: it isn't the whole set of size 27
28 ≈ 1.20 * 10
40 anymore, but only of size 27 * 28 = 756...
Another advantage: you only have to call your random generator twice for each child, while a straight-forward implementation of the letter-mutating process take (1+μ)*28 of these costly calls per child - though this number can be reduced to (1+28*μ) calls per child....
So, one parameter less to tweak: though the number of children is set to 100 in this program, this can be changed easily.

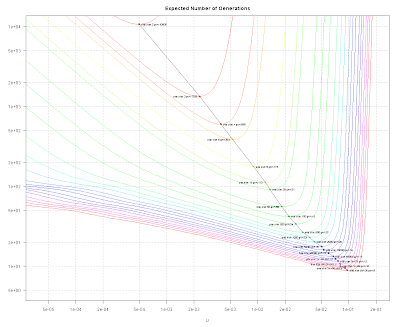
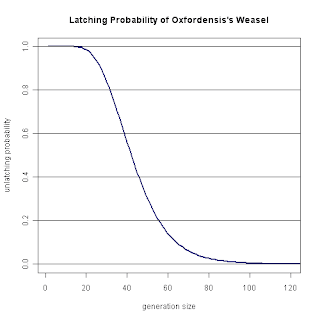
But which value to chose for the remaining parameter - the size of the population? The bigger the size of the population, the less generations (black line) it takes to complete the search. So, make it big? No, not necessarily: commonly, you want your program to be fast. Therefore, you should try to reduce the number of queries (blue line), i.e, the number of mutated strings - which is the number of evaluations of the fitness function, too. Mutating at random, and calculating the fitness function, that's what's taking time.
I suppose if you fool around with the program for a while, you'll quickly find out that the optimal size of generations in the sense above is about 50 - and an exact calculation leads to an average of 3931 queries for a population size of 49 as an optimum (σ = 648.04).
Weasel 2
Well, this beast is boring. BORING. Look how it works for the target "METHINKS IT IS LIKE A WEASEL":
- Chose random string
- make new string by copying old string one time, changing exactly one letter at random
- chose string from old and new string with most correct letters in place
- is the number of correct letters 28? Then STOP. Otherwise:
- goto 2
It's just a randomized version of the
hangman game, taking 2969 steps on average (σ = 959.2). And it's what W. Dembski and R. Marks call
Optimization by Mutation With Elitism in their current paper:
3) Optimization by Mutation With Elitism: Optimization by
mutation with elitism is the same as optimization by mutation
in Section III-F2 with the following change. One mutated
child is generated. If the child is better than the parent, it
replaces the parent. If not, the child dies, and the parent
tries again. Typically, this process gives birth to numerous
offspring, but we will focus attention on the case of a single
child. We will also assume that there is a single bit flip per
generation.
Conclusions
Could these be the programs used by R. Dawkins in his book
The Blind Watchmaker? The first one would fit his algorithm, and with a population size, it would take 47.6 generations on average (σ= 11.7). And what's about the BBC video? If the second version was used for this, I'd regard it at best as a visual effect, as it doesn't match Dawkins's algorithm. And yes, it is (implicitly) latching :-)